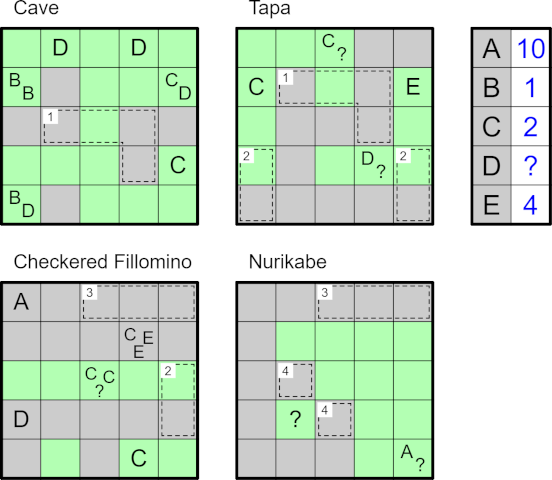
There are four puzzles: Cave, Checkered Fillomino, Nurikabe, and Tapa. The solver must determine which puzzle corresponds to which grid.
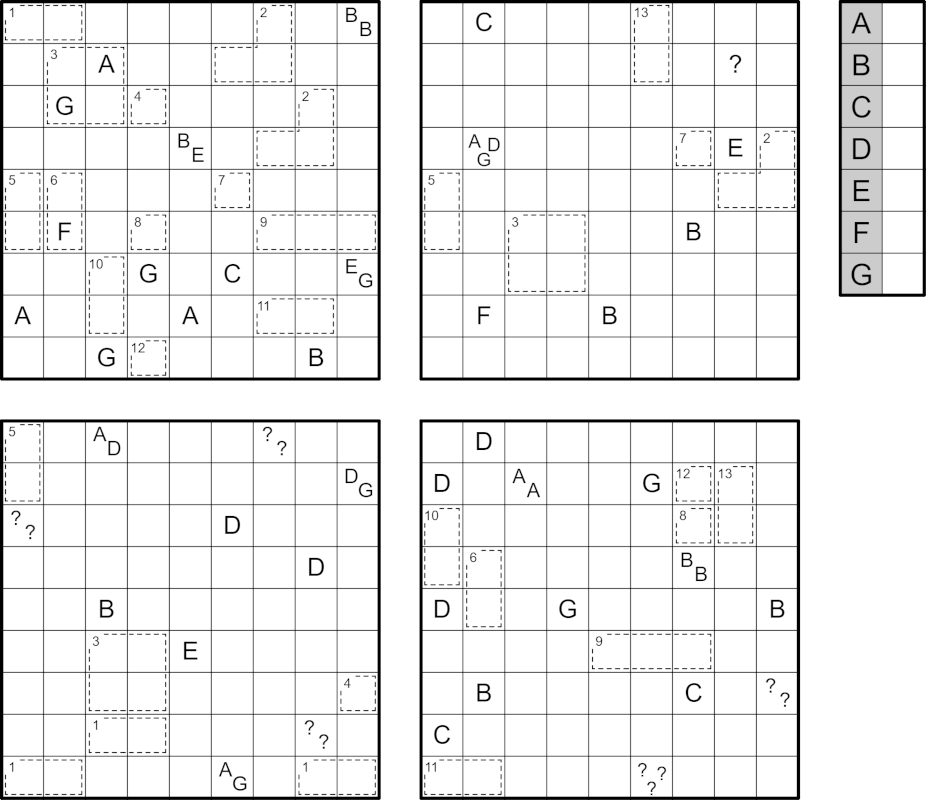
The cipher contains 7 letters (A-G). 6 of them must replaced by unique positive integers, while the last is an 'irrwisch': it replaces a different positive integer in every occurrence. A '?' may represent any positive integer. For every puzzle except the Tapa, the value of a clue is the sum of the integer values in the cell.
Each set of cages with the same number in the top-left corner must have identical shading.
Cave: Shade some cells so that the shaded cells are all connected orthogonally by other shaded cells to the edge of the grid, and the remaining unshaded cells form one orthogonally connected area. Clues cannot be shaded, and indicate the total number of unshaded cells that can be seen in a straight line vertically or horizontally, including itself.
Checkered Fillomino: Divide the grid into regions of orthogonally connected cells. Two regions of the same size may not share an edge. Shade some cells such that each region is either fully shaded or fully unshaded, and no two shaded regions or two unshaded regions share an edge. Clued cells must belong to a region containing the indicated number of cells.
Nurikabe: Shade some cells so that all shaded cells form one orthogonally connected area and no 2x2 region is entirely shaded. Clues cannot be shaded, and every orthogonally connected area of unshaded cells contains exactly one clue, the value of which indicates the size of the area.
Tapa: Shade some cells so that all shaded cells form one orthogonally connected area and no 2x2 region is entirely shaded. Clues cannot be shaded, and indicate the lengths of the blocks of consecutive shaded cells in the (up to) eight cells surrounding the clue.
Here is an example to demonstrate the rules. (This is not intended to be solvable.)